Certifying Interpreters in Racket
When I began programming, I read a copy of Richard Steven’s “Programming in the UNIX Environment.” Ultimately, my early experimentations with C were a failure; however, I later read David Beazley’s “Python: Essential Reference,” and was quickly able to pick up the UNIX API via it’s much simpler (admittedly, largely due to Beazley’s writing) Python counterpart. After teaching my undergraduate PL courses in Scheme variants these past few years I have wondered if we can understand type theory’s operationalization (via proof objects) using a similar shift in perspective.
Here, I rigorously define an interpreter which produces a certificate of its own correctness—assuming you trust the correctness of our metalanguage, which (in the interests of appeasing the more skeptical among us) we treat as S-expression comparison. Here I use Racket, but any similar dynamic language with matching (or, if in OO, virtual methods) would work to illustrate the key ideas. I do use Racket’s contracts to check certificates, though other implementations could defer this to the end or even elide checking entirely.
The Language
;; Specification of IfArith's syntax as a Racket predicate
(define (expr? e)
(match e
[(? nonnegative-integer? n) #t]
[(? symbol? x) #t]
[`(let ,(? symbol? x) ,(? expr? e) ,(? expr? e-body))]
[`(plus ,(? expr? e0) ,(? expr? e1)) #t]
[`(not ,(? expr? e-guard)) #t]
[`(if0 ,(? expr? e0) ,(? expr? e1) ,(? expr? e2)) #t]
[_ #f]))
(define e0 '(plus 2 1)) ;; 3
(define e1 '(plus 1 (if0 0 1 2))) ;; 2
(define e2 '(let x (plus 0 0) (plus x 1))) ;; 1
(define e3 '(let x (plus 0 (if0 (plus 0 0) 1 0)) (plus x 0))) ;; 1
The Proofs
Now the tricky part: we need to think about what proofs for evaluation
of terms in our little language look like. To be precise about it, we
need to define a relation: e, ρ ⇓ v, such that e is an expression,
ρ is an environment (mapping variables to values) and v is a
value. To be constructive about it, we need to algebraically define a
structure representing proofs that the evaluation of e in ρ
evaluates to v. Following the Scheme tradition of homoiconicity, we
represent proofs as S-expressions themselves; inference rules using
pattern matching over these S-expressions to mirror the natural
deduction (big-step) style in which we would write our semantics on
paper. As an example, here’s a derivation of (if0 0 (plus 1 1) 0).
(⇓-if-true
(⇓-const -----
(0 ∅ ⇓ O))
(⇓-plus
(⇓-const -----
(1 ∅ ⇓ (S O)))
(⇓-const -----
(1 ∅ ⇓ (S O)))
(plus -----
(= (+ (S O) (S O)) (S (S O))))
-----
((plus 1 1) ∅ ⇓ (S (S O))))
-----
((if0 0 (plus 1 1) 0) ∅ ⇓ (S (S O))))
Racket’s pattern matcher is, of course, very different than a more elaborate matcher centered around higher-order unification in a statically-typed setting. Manually explicating the unification becomes a bit of a chore after a while; certainly a rebuke to the thought of using this as a serious strategy for type theory, but at the same time precisely the reason we’re doing it this way.
Of course it would be possible (especially in such a simple semantics
as this) to define e, ρ ⇓ v using substitution to implement
variables; I explicitly materialize environments to (a) anticipate
closures (later) and (b) present a representational challenge upon
which I would like to expand a bit. Of course, using Racket as our
metalanguage, we could simply use hashes for environments. But
remember—we are trying to appease the pedants among us, thus
representation must be as symbolic as possible. Similarly, I represent
the naturals symbolically. I do allow myself a serious concession: I
internalize plus, as I elide fix in the source language. If this
disappoints you, I would say there’s no fundamental barrier; we could
easily-enough (via environments) implement application and then a
fixed-point combinator.
;; naturals
(define (nat? n)
(match n ['O #t] [`(S ,(? nat? n)) #t] [_ #f]))
(define/contract (num->nat n)
(-> nonnegative-integer? nat?)
(match n
[0 'O]
[n `(S ,(num->nat (- n 1)))]))
(define/contract (nat->num n)
(-> nat? nonnegative-integer?)
(match n
['O 0]
[`(S ,x) (add1 (nat->num x))]))
(define/contract (nat-add s0 s1)
(-> nat? nat? nat?)
(match s0
['O s1]
[`(S ,s0+) `(S ,(nat-add s0+ s1))]))
To represent environments we define (a) a predicate dictating valid
structure for environments and (b) a predicate, (env-maps? ρ x v
pf), which defines the structure of valid proofs showing that
environment ρ maps variable x to value v. Both of these are in
the de-facto “trusted computing base,” in the sense that if your
definition of proofs is broken (i.e., don’t faithfully capture what
you want to prove) then it doesn’t matter that your interpreter
produces proofs. And, of course, this is the biggest drawback of using
an untyped language to do this—we only get some rough syntactic
checking, similar to tools such as Ott but not dependently-typed
languages or provers. To avoid completely defeating the purpose of our
exercise here, I have followed a bit of a trick to rely minimally on
Racket as a metatheory: because many objects internal to the semantics
(e.g., numbers, environments, and proofs) are represented purely
symbolically (as S-expressions), we primarily rely upon Racket for
S-expression equality and dispatch (matching). Aside from plus our
semantics uses a very small subset of Racket: I believe essentially
either (equivalently) existential fixed-point logic (of a Herbrand
base comprising S-expressions) or constrained horn clauses (whose
background logic includes S-expression equality and
structurally-recursive addition).
;; environments
(define (environment? ρ)
(match ρ
['∅ #t]
[`(↦ ,(? environment? ρ+) ,(? symbol? x) ,(? value? v)) #t]
[_ #f]))
;; environment lookup -- predicate (inductive defn.)
(define/contract (env-maps? pf ρ x v)
(-> any/c environment? symbol? value? boolean?)
(match pf
[`(↦-hit
------
(↦ ,ρ ,x0 ,v0))
(and (equal? x0 x) (equal? v0 v))]
[`(↦-miss
,next-pf
-----
(↦ ,ρ ,x0 ,_))
(and (not (equal? x0 x))
(env-maps? next-pf ρ x v))]
[_ #f]))
The implementation of (⇓ pf e ρ v) follows its natural deduction
counterpart (which I have not written down, but try to stylize via my
spacing). Our procedure checks the proof, recursively calling itself
to check subproofs—mirroring the top-down process you may follow on
a whiteboard to check the proof yourself, though Reynolds points out
that the order of sub-checks is inherited from the metalanguage (i.e.,
Racket’s control flow).
;; proofs of evaluation
(define/contract (⇓ pf e ρ v)
(-> any/c expr? environment? value? boolean?)
(match pf
;; Const
[`(⇓-const
-----
(,(? nonnegative-integer? n) ,ρ+ ⇓ ,v+))
(and (equal? (num->nat n) v) (equal? v v+) (equal? ρ+ ρ))]
...
Checking proofs for constants is easy. The rest of the rules follow
their natural deduction counterparts; the tedious part is the
administrative overhead required to implement the store-passing
construction. Of course my code is a bit smelly here; the ad-hoc use
of consequent points to a much cleaner refactoring that elides using
pairs of a return value and its proof in favor of projecting the value
from the proof, but the point here is to stick to what I think I’d end
up with doing it in an interactive proof assistant.
;; Var
[`(⇓-var ,proof-x-in-ρ
-----
(,(? symbol? x) ,(? environment? ρ+) ⇓ ,(? value? v+)))
(and (equal? ρ+ ρ) (equal? v+ v) (env-maps? proof-x-in-ρ ρ x v))]
;; Let
[`(⇓-let
,proof-e0
,proof-e1
-----
((let ,x ,e0 ,e1) ,(? environment? ρ+) ⇓ ,(? value? v+)))
(and (equal? v+ v) (equal? ρ+ ρ)
(⇓ proof-e0 e0 ρ (last (consequent proof-e0)))
(⇓ proof-e1 e1 `(↦ ,ρ ,x ,(last (consequent proof-e0)))
(last (consequent proof-e1))))]
;; Plus
[`(⇓-plus
,proof-e0
,proof-e1
(plus ----- (= (+ ,v0+ ,v1+) ,v-r))
-----
((plus ,e0 ,e1) ,ρ+ ⇓ ,v-r))
#:when (and (equal? v-r v) (equal? ρ+ ρ))
(define v0 (last (consequent proof-e0)))
(define v1 (last (consequent proof-e1)))
(and (⇓ proof-e0 e0 ρ v0)
(⇓ proof-e1 e1 ρ v1)
(equal? v0+ v0)
(equal? v1+ v1)
(equal? v-r (nat-add v0 v1)))]
;; Not
[`(⇓-not-0
,proof-e0
-----
((not ,e0) ,ρ ⇓ O))
(define v0+ (match (consequent proof-e0) [`(,_ ,_ ⇓ ,v) v]))
(and (equal? v0+ v) (not (equal? v 'O)) (⇓ proof-e0 e0 ρ v))]
[`(⇓-not-1
,proof-e0
-----
((not ,e0) ,ρ ⇓ (S O)))
(define v0+ (match (consequent proof-e0) [`(,_ ,_ ⇓ ,v) v]))
(and (equal? v0+ v) (equal? v 'O) (⇓ proof-e0 e0 ρ v))]
;; If-True
[`(⇓-if-true
,proof-guard-true
,proof-e1-v-res
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v))
(match (consequent proof-guard-true)
[`(,_ ,_ ⇓ O)
(and (⇓ proof-guard-true e0 ρ 'O)
(⇓ proof-e1-v-res e1 ρ v))])]
;; If-False
[`(⇓-if-false
,proof-guard-false
,proof-e1-v-res
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v+))
#:when (equal? v+ v)
(match (consequent proof-guard-false)
[`(,_ ,_ ⇓ ,n)
(and (not (equal? n 'O))
(⇓ proof-guard-false e0 ρ n)
(⇓ proof-e1-v-res e1 ρ v))])]
The Programs
Compared to the checking, writing the proofs is surprisingly
straightforward—even pleasant (okay; maybe not pleasant). A common
idiom when writing certified (proof-backed) code is the notion of
returning an existential, i.e., a witness alongside its proof. Of
course, the key challenge in writing certified code is convincing
yourself of its correctness. There are a variety of ways you could do
this: you could inspect the output of the evaluator I write and ensure
that they match the specification, for example. However, for full
clarity, I will use Racket’s contract system, which allows dynamic
checking—this allows us to check the correctness of our evaluators
as we go, but of course won’t prove correctness across all runs, and
using define/contract also interposes the check at every callsite
(a serious overhead), though I am sure you can use your imagination
about how this could be made faster.
Let’s start with environments, writing a function (lookup ρ x),
which returns a proof that x returns some value v–if it doesn’t,
we would just throw a dynamic error due to a match failure–we are
posting a proof exists. We can write a contract to ensure that the
code we use to do this is correct. Racket’s default arrow contract
combinator, ->, is not powerful enough to express dependent
contracts, where a property of the result depends on one of the
inputs. However, Racket’s more powerful ->i does allow dependent
contracts, allowing us to write a version of lookup which both
computes what we want and checks to ensure its correctness:
;; decision procedure for lookup -- returns witness and proof of inclusion
(define/contract (lookup ρ x)
;; v---- domain ----v
(->i ([ρ environment?] [x symbol?])
;; range -- produces a proof dependent on ρ,x
[result (ρ x)
(match-lambda [`(,(? value? v) . ,pf) (env-maps? pf ρ x v)]
[_ #f])])
(match ρ
[`(↦ ,ρ1 ,x1 ,v) #:when (equal? x1 x)
`(,v . (↦-hit ------ (↦ ,ρ ,x ,v)))]
[`(↦ ,ρ1 ,x1 ,v) #:when (not (equal? x1 x))
(match (lookup ρ1 x)
[`(,v . ,pf)
`(,v . (↦-miss ,pf ----- (↦ ,ρ1 ,x1 ,v)))])]))
Finally, the interpreter itself—unadorned by the ceremony and pedantics of low-level unification checking—is surprisingly unintimidating and to-the-point.
;; produce a value alongside a proof of its correctness
(define/contract (eval e ρ)
;; contract: returns pair of value and proof of its derivation
(->i ([e expr?] [ρ environment?])
[result (e ρ)
(lambda (witness-pf) (match witness-pf
[`(,(? value? v) . ,pf) (⇓ pf e ρ v)]
[_ #f]))])
(match e
[(? nonnegative-integer? n)
(cons (num->nat n)
`(⇓-const
-----
(,n ,ρ ⇓ ,(num->nat n))))]
[(? symbol? x)
(match (lookup ρ x)
[`(,v . ,pf)
(cons v `(⇓-var
,pf
-----
(,x ,ρ ⇓ ,v)))])]
[`(let ,x ,e ,eb)
(match (eval e ρ)
[`(,v . ,pf-e)
(match (eval eb `(↦ ,ρ ,x ,v))
[`(,v-res . ,pf-v)
(cons v-res
`(⇓-let
,pf-e
,pf-v
-----
((let ,x ,e ,eb) ,ρ ⇓ ,v-res)))])])]
[`(plus ,e0 ,e1)
(match-define `(,v0 . ,pf-v0) (eval e0 ρ))
(match-define `(,v1 . ,pf-v1) (eval e1 ρ))
(define v-res (nat-add v0 v1))
(cons v-res
`(⇓-plus
,pf-v0
,pf-v1
(plus ----- (= (+ ,v0 ,v1) ,v-res))
-----
((plus ,e0 ,e1) ,ρ ⇓ ,v-res)))]
[`(not ,e)
(match (eval e ρ)
[`(0 . ,pf-e)
(cons '(S O)
`(⇓-not-1
,pf-e
-----
((not ,e) ρ ⇓ (S O))))]
[`(,v0 . ,pf-e)
(cons 'O
`(⇓-not-0
,pf-e
-----
((not ,e) ρ ⇓ O)))])]
[`(if0 ,e0 ,e1 ,e2)
(match (eval e0 ρ)
[`(O . ,pf-e0)
(match (eval e1 ρ)
[`(,v . ,pf-v)
(cons v
`(⇓-if-true
,pf-e0
,pf-v
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v)))])]
[`(,n . ,pf-e0)
(match (eval e2 ρ)
[`(,v . ,pf-v)
(cons v
`(⇓-if-false
,pf-e0
,pf-v
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v)))])])]))
Visualizing our Proofs
Alright, so now our interpreter writes proofs–what do they look like? Thankfully, we used S-expressions.
;; nice latex; comment out the labels by adding a % before \\tiny
(define (pf->tex pf)
(define name (first pf))
(define antecedents (reverse (list-tail (reverse (list-tail (cdr pf) 0)) 2)))
(foldr
(lambda (k v acc) (string-replace acc k v))
(format " \n \\frac{ ~a }{ \\texttt{ ~a } }}"
name
(string-join (map pf->tex antecedents) "\\,")
(consequent pf))
'("⇓" "∅" "↦")
'("\\ensuremath{\\Downarrow}" "\\ensuremath{\\emptyset}"
"\\ensuremath{\\mapsto}")))
Here’s the complete derivation of ((plus 1 (if0 0 1 2))):
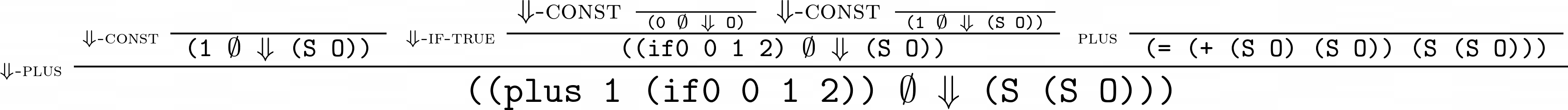
And a longer program where I had to remove the rule names in rendering…
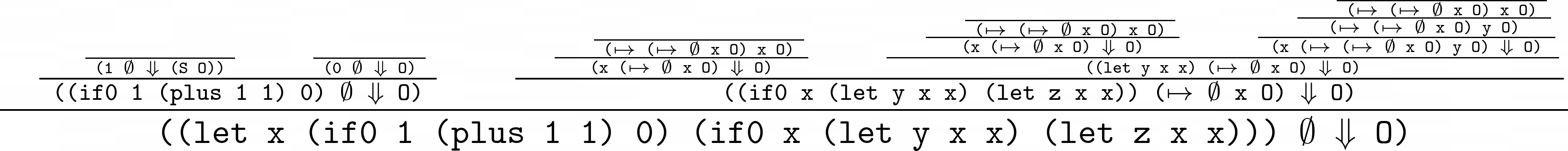
Metatheoretic Concessions for the Working Programmer
Obviously we would never write an interpreter in Racket the way we did
above: there’s too much extraneous math (i.e., the proof objects). I
think it’s surprising, though, to see how much more direct the code
becomes by (a) erasing the proofs, (b) implementing the environment as
hashes, and (c) relying upon racket’s built-in representation of
numbers. The biggest burden in my implementation is obviously (a), as
I have explicated the proofs via cons. Tighter implementations exist
that would hide the ugliness via (say) monads. Eliminating proofs also
eliminates a lot of administrative matching and in some places allows
to make tail calls to eval where we couldn’t before, giving us a
textbook metacircular interpreter. I think it is interesting to see
just how directly a translation it is: I systematically removed each
feature (in the same way an extractor would) to achieve the simpler
implementation.
(define (eval-simpl e ρ)
(match e
[(? nonnegative-integer? n) n]
[(? symbol? x) (hash-ref ρ x)]
[`(let ,x ,e ,eb) (eval-simpl eb (hash-set ρ x (eval-simpl e ρ)))]
[`(plus ,e0 ,e1) (+ (eval-simpl e0 ρ) (eval-simpl e1 ρ))]
[`(not ,e)
(match (eval-simpl e ρ)
[0 1]
[_ 0])]
[`(if0 ,e0 ,e1 ,e2)
(match (eval-simpl e0 ρ)
[0 (eval-simpl e1 ρ)]
[_ (eval-simpl e2 ρ)])]))
Conclusion
Do I think this is the future of dependently typed programming? Of anything? Perhaps both no. Racket is not a particularly appealing implementation language for type theory and its pattern matching is not designed to scale to settings where higher-order unification is of concern to the user. Similarly, this code has serious algorithmic inefficiencies; plenty of the proof checking could be memoized, and perhaps some simple contract trick would achieve this (though other evaluation strategies could, e.g., use tabling in the metatheory). I largely wrote this up to motivate my thoughts on (the potential of) explaining the operationalization of proof objects to students as an extension of operational semantics in the untyped setting I teach in my class. Perhaps this will help someone draw connections between operational semantics and proof objects, though I hesitate to say type theory, broadly.
Ultimately I did manage to find a lot of bugs in my implementation of the interpreter using the contracts. Obviously, though, I was driving the process by generating terms and not using a systematic methodology of proving the correctness–I have tried to say that the interpreter generates certificates, but it is of course not certified. It’s a fun exercise, though–you can read the full code yourself below. I think there are a few follow ups that could be done from here if you are interested in experimenting with the code. Adding closures and application, for example, should not be too hard; I may illustrate that in my course next term.
Thanks to Quinn Wilton for some corrections to the phrasing in this post.
The Code
;; self-certifying interpreters, summer 2022, kris micinski
#lang racket
;; naturals
(define (nat? n)
(match n ['O #t] [`(S ,(? nat? n)) #t] [_ #f]))
(define/contract (num->nat n)
(-> nonnegative-integer? nat?)
(match n
[0 'O]
[n `(S ,(num->nat (- n 1)))]))
(define/contract (nat->num n)
(-> nat? nonnegative-integer?)
(match n
['O 0]
[`(S ,x) (add1 (nat->num x))]))
(define/contract (nat-add s0 s1)
(-> nat? nat? nat?)
(match s0
['O s1]
[`(S ,s0+) `(S ,(nat-add s0+ s1))]))
;; values are nats
(define value? nat?)
;; expressions
(define (expr? e)
(match e
[(? nonnegative-integer? n) #t]
[(? symbol? x) #t]
[`(let ,(? symbol? x) ,(? expr? e) ,(? expr? e-body)) #t]
[`(plus ,(? expr? e0) ,(? expr? e1)) #t]
[`(not ,(? expr? e-guard)) #t]
[`(if0 ,(? expr? e0) ,(? expr? e1) ,(? expr? e2)) #t]
[_ #f]))
;; environments
(define (environment? ρ)
(match ρ
['∅ #t]
[`(↦ ,(? environment? ρ+) ,(? symbol? x) ,(? value? v)) #t]
[_ #f]))
;; environment lookup -- predicate (inductive defn.)
(define/contract (env-maps? pf ρ x v)
(-> any/c environment? symbol? value? boolean?)
(match pf
[`(↦-hit
------
(↦ ,ρ ,x0 ,v0))
(and (equal? x0 x) (equal? v0 v))]
[`(↦-miss
,next-pf
-----
(↦ ,ρ ,x0 ,_))
(and (not (equal? x0 x))
(env-maps? next-pf ρ x v))]
[_ #f]))
;; decision procedure for lookup -- returns witness and proof of inclusion
(define/contract (lookup ρ x)
;; v---- domain ----v
(->i ([ρ environment?] [x symbol?])
;; range -- produces a proof dependent on ρ,x
[result (ρ x)
(lambda (witness-pf) (match witness-pf
[`(,(? value? v) . ,pf) (env-maps? pf ρ x v)]
[_ #f]))])
(match ρ
[`(↦ ,ρ1 ,x1 ,v) #:when (equal? x1 x)
`(,v . (↦-hit ------ (↦ ,ρ ,x ,v)))]
[`(↦ ,ρ1 ,x1 ,v) #:when (not (equal? x1 x))
(match (lookup ρ1 x)
[`(,v . ,pf)
`(,v . (↦-miss ,pf ----- (↦ ,ρ1 ,x1 ,v) ))])]))
; (lookup '(↦ (↦ ∅ x O) y (S O)) 'x)
;; we will now follow the style '(name atecedent0 ... ----- consequent)
(define (consequent judgement) (last judgement))
;; predicate -- inductive definition of evaluation relation
(define/contract (⇓ pf e ρ v)
(-> any/c expr? environment? value? boolean?)
(match pf
;; Const
[`(⇓-const
-----
(,(? nonnegative-integer? n) ,ρ+ ⇓ ,v+))
#:when (and (equal? (num->nat n) v) (equal? ρ+ ρ) (equal? v v+))
#t]
;; Var
[`(⇓-var ,proof-x-in-ρ
-----
(,(? symbol? x) ,(? environment? ρ+) ⇓ ,(? value? v+)))
#:when (and (equal? ρ+ ρ) (equal? v+ v))
(env-maps? proof-x-in-ρ ρ x v)]
;; Let
[`(⇓-let
,proof-e0
,proof-e1
-----
((let ,(? symbol? x) ,(? expr? e0) ,(? expr? e1)) ,(? environment? ρ+) ⇓ ,(? value? v+)))
#:when (equal? v+ v) (equal? ρ+ ρ)
(and (⇓ proof-e0 e0 ρ (last (consequent proof-e0)))
(⇓ proof-e1 e1 `(↦ ,ρ ,x ,(last (consequent proof-e0))) (last (consequent proof-e1))))]
;; Plus
[`(⇓-plus
,proof-e0
,proof-e1
(plus ----- (= (+ ,v0+ ,v1+) ,v-r))
-----
((plus ,e0 ,e1) ,ρ+ ⇓ ,v-r))
#:when (and (equal? v-r v) (equal? ρ+ ρ))
(define v0 (last (consequent proof-e0)))
(define v1 (last (consequent proof-e1)))
(and (⇓ proof-e0 e0 ρ v0)
(⇓ proof-e1 e1 ρ v1)
(equal? v0+ v0)
(equal? v1+ v1)
(equal? v-r (nat-add v0 v1)))]
;; Not
[`(⇓-not-0
,proof-e0
-----
((not ,e0) ,ρ ⇓ O))
(define v0+ (match (consequent proof-e0) [`(,_ ,_ ⇓ ,v) v]))
(and (equal? v0+ v) (not (equal? v 'O)) (⇓ proof-e0 e0 ρ v))]
[`(⇓-not-1
,proof-e0
-----
((not ,e0) ,ρ ⇓ (S O)))
(define v0+ (match (consequent proof-e0) [`(,_ ,_ ⇓ ,v) v]))
(and (equal? v0+ v) (equal? v 'O) (⇓ proof-e0 e0 ρ v))]
;; If-True
[`(⇓-if-true
,proof-guard-true
,proof-e1-v-res
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v))
(match (consequent proof-guard-true)
[`(,_ ,_ ⇓ O)
(and (⇓ proof-guard-true e0 ρ 'O)
(⇓ proof-e1-v-res e1 ρ v))])]
;; If-False
[`(⇓-if-false
,proof-guard-false
,proof-e1-v-res
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v+))
#:when (equal? v+ v)
(match (consequent proof-guard-false)
[`(,_ ,_ ⇓ ,n)
(and (not (equal? n 'O))
(⇓ proof-guard-false e0 ρ n)
(⇓ proof-e1-v-res e1 ρ v))])]
[_ #f]))
;;
;; Self-certifying interpreter
;;
;; produce a value alongside a proof of its correctness
(define/contract (eval e ρ)
;; contract: returns pair of value and proof of its derivation
(->i ([e expr?] [ρ environment?])
[result (e ρ)
(lambda (witness-pf) (match witness-pf
[`(,(? value? v) . ,pf) (⇓ pf e ρ v)]
[_ #f]))])
(match e
[(? nonnegative-integer? n)
(cons (num->nat n)
`(⇓-const
-----
(,n ,ρ ⇓ ,(num->nat n))))]
[(? symbol? x)
(match (lookup ρ x)
[`(,v . ,pf)
(cons v `(⇓-var
,pf
-----
(,x ,ρ ⇓ ,v)))])]
[`(let ,x ,e ,eb)
(match (eval e ρ)
[`(,v . ,pf-e)
(match (eval eb `(↦ ,ρ ,x ,v))
[`(,v-res . ,pf-v)
(cons v-res
`(⇓-let
,pf-e
,pf-v
-----
((let ,x ,e ,eb) ,ρ ⇓ ,v-res)))])])]
[`(plus ,e0 ,e1)
(match-define `(,v0 . ,pf-v0) (eval e0 ρ))
(match-define `(,v1 . ,pf-v1) (eval e1 ρ))
(define v-res (nat-add v0 v1))
(cons v-res
`(⇓-plus
,pf-v0
,pf-v1
(plus ----- (= (+ ,v0 ,v1) ,v-res))
-----
((plus ,e0 ,e1) ,ρ ⇓ ,v-res)))]
[`(not ,e)
(match (eval e ρ)
[`(0 . ,pf-e)
(cons '(S O)
`(⇓-not-1
,pf-e
-----
((not ,e) ρ ⇓ (S O))))]
[`(,v0 . ,pf-e)
(cons 'O
`(⇓-not-0
,pf-e
-----
((not ,e) ρ ⇓ O)))])]
[`(if0 ,e0 ,e1 ,e2)
(match (eval e0 ρ)
[`(O . ,pf-e0)
(match (eval e1 ρ)
[`(,v . ,pf-v)
(cons v
`(⇓-if-true
,pf-e0
,pf-v
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v)))])]
[`(,n . ,pf-e0)
(match (eval e2 ρ)
[`(,v . ,pf-v)
(cons v
`(⇓-if-false
,pf-e0
,pf-v
-----
((if0 ,e0 ,e1 ,e2) ,ρ ⇓ ,v)))])])]))
;; nice latex; comment out the labels by adding a % before \\tiny
(define (pf->tex pf)
(define name (first pf))
(define antecedents (reverse (list-tail (reverse (list-tail (cdr pf) 0)) 2)))
(foldr
(lambda (k v acc) (string-replace acc k v))
(format " \n \\frac{ ~a }{ \\texttt{ ~a } }}"
name
(string-join (map pf->tex antecedents) "\\,")
(consequent pf))
'("⇓" "∅" "↦")
'("\\ensuremath{\\Downarrow}" "\\ensuremath{\\emptyset}" "\\ensuremath{\\mapsto}")))
(define (derive e)
(displayln (pf->tex (cdr (eval e '∅)))))
;; examples
;(derive '(let x (plus 0 (if0 (plus 0 0) 1 0)) (plus x 0)))
;(derive '(plus 1 (if0 0 1 2)))
;(derive '(let x (plus 0 0) (plus x 1)))
(define (eval-simpl e ρ)
(match e
[(? nonnegative-integer? n) n]
[(? symbol? x) (hash-ref ρ x)]
[`(let ,x ,e ,eb)
(eval-simpl eb (hash-set ρ x (eval-simpl e ρ)))]
[`(plus ,e0 ,e1) (+ (eval-simpl e0 ρ) (eval-simpl e1 ρ))]
[`(not ,e)
(match (eval-simpl e ρ)
[0 1]
[_ 0])]
[`(if0 ,e0 ,e1 ,e2)
(match (eval-simpl e0 ρ)
[0 (eval-simpl e1 ρ)]
[_ (eval-simpl e2 ρ)])]))